If Naoh Is Added To Water, How Does [h+] Change?

BUFFERS

In the previous section, the Henderson–Hasselbalch equation was introduced, which is handy for dealing with pH calculations involving weak acids and their conjugate bases. This equation is very important to biochemists, who are always concerned with keeping proteins and other biological molecules in the lab at their proper pH. Indeed, a solution that contains a weak acid and its conjugate base has the special property of being able to resist changing its pH when either a base of operations or an acid is added to it. Such a solution is called a buffer because the solution is protected, or buffered, from pH changes even when H₃O⁺ or OH^– ions are added to the solution. Buffers help biochemists written report biomolecular reactions in the laboratory by stabilizing the pH of solutions used for experiments.

To get a better sense of the utility of buffer solutions, let's compare the difference betwixt adding a strong base to a buffered solution, and calculation the aforementioned amount of strong base of operations to water. This is done in the examples below.

Example v

If 10 mL of 1M NaOH are added to one liter of a buffer that is 0.iii M acetic acid and 0.2 M sodium acetate (Na⁺CH₃COO^–), how much does the pH change? The pK_a for acetic acid is 4.76.

Reply:

In the original solution, acetic acid is the weak acid, and acetate is the conjugate base of operations. Thus, [base] = 0.2 Yard, and [acid] = 0.iii One thousand.

Using the Henderson–Hasselbalch equation,

pH	=	pKa	+	log	[Base]
					[Acid]

pH = 4.72 + log (0.2/0.3)
pH = 4.54

NaOH is a strong base, and dissociates completely. Therefore, calculation the strong base of operations results in

(0.01 liter)(1 Thousand) = 0.01 moles of OH^– ions into the solution.

All of the OH^– ions will react with the acetic acid to form acetate ions:

CH₃COOH + OH^– CH₃COO^– + H₂O

Thus, when NaOH is added, the number of acetic acid molecules in the solution will subtract, but the number of acetate molecules in the solution will increment. In this instance, 0.01 moles of acetic acid volition exist used up to neutralize the 0.01 moles of OH^–, and this will form 0.01 moles of acetate ion in the solution.

At the end of the reaction:

Moles of acetic acid	=	moles of acetic acid before the reaction	–	moles of acetic acid used up in the reaction
	=	0.3 moles	–	0.01 moles	=	0.29 moles
Moles of acetate	=	moles of acetate before the reaction	+	moles of acetate made in the reaction
	=	0.2 moles	+	0.01 moles	=	0.21 moles

Now we are almost set up to plug back into the Henderson–Hasselbalch equation to observe the new pH of the solution. We just need to retrieve that the volume has changed slightly, from 1 liter (k mL) to ane liter plus 10 mL (1010 mL). The Henderson–Hasselbalch equation requires that the [Base] and [Acid] exist molar (M, or mol/L) quantities. Still, notice how that because both the acid and base species are in the aforementioned volume, the volume correction cancels out:

pH	=	pKa	+	log	[Base]
					[Acrid]

pH	=	pKa	+	log	(0.29 moles/1.01 liter)
					0.21 moles/ 1.01 liter)

pH = four.72 + log one.38
pH = 4.86
The pH modify is iv.86 – 4.54 = 0.32 units.

Example 6

How much does the pH change when 10 mL of ane Grand NaOH is added to 1 liter of water?

Answer: Pure water has a pH of 7.0. NaOH is a strong base, and once it has been added to the water it will dissociate completely, contributing 0.01 moles OH^– ions, in a full book of 1010 mL ( 1 liter plus the 10 mL NaOH added). Thus,

[OH^–] = 0.01 moles / 1.01 liter = 0.0099 M

Plugging into the K_w expression: [OH^–][H₃O⁺] = 10^–xiv:

(0.0099)[H_threeO⁺] = 10^–fourteen
[H₃O⁺] = one.01 10 x^–12 M

Then plugging into the pH equation:

pH = – log [H⁺]
pH = – log 1.01 x ten^–12
pH = eleven.99

The pH has shifted from the neutral pH of 7 for the pure water to a pH of near 12 with the NaOH added, a shift of 5 pH units!

Buffering agents stabilize the pH of aqueous solutions

In example 5, the pH of the buffer solution changed past less than 0.5 units when the NaOH was added. Yet adding the same amount of NaOH to pure water resulted in a 5 unit pH shift in example half dozen. Clearly, the conjugate acrid/base pair was able to protect the solution from a large alter in pH.

A buffer is a solution that resists a change in pH when acids or bases are added to it.

How is this possible? Buffers work by acting a little bit like a sponge, soaking upward excess H_iiiO⁺ or OH^– ions when they are added to a solution. The dissociation reaction for acetic acrid shows that a solution of acetic acid contains acetate ions:

CH₃COOH + H₂O CH₃COO^– + H₃O⁺

How exercise acerb acid and the acetate ion work to buffer the solution? If a potent acid, such every bit muriatic acid, is added to this buffer, the H₃O⁺ ions generated will react with the acetate ions, removing them from the solution:

CH3COO–	+	H3O+		CH3COOH	+	H2O
acetate ion		hydronium ion		acetic acid		water

Similarly, if a strong base, generating lots of OH^– ions, were added to the acetic acid buffer solution

CHiiiCOOH	+	OH–		CHiiiCOO–	+	H2O
acetic acid		hydroxide ion		acetate acid		water

The OH^– ions are removed via a reaction with acetic acid. It is important to call back that buffers cannot maintain their pH indefinitely equally more than acid or base is added. Imagine slowly pouring a bucketful of h2o onto a small sponge on the kitchen floor. At first, every bit the water pours out of the bucket it is absorbed by the sponge, keeping the kitchen floor dry. But once the sponge is soaked through, it can hold no more and the h2o spills onto the floor equally fast as if the sponge weren't at that place. In the same manner, buffers will protect the pH of the solution to some extent, simply if they are inundated by large amounts of H₃O⁺ or OH^– ions, all the bachelor cohabit acid or base of operations molecules volition have been used upwards and pH changes will rapidly occur.

Thus, buffers only piece of work as long as the amount of cohabit acid and base ions are large compared to the H₃O⁺amount of or OH^– ions to be removed. Remember from the Henderson-Hasselbalch equation (department 5) that the numbers of conjugate acrid molecules is equal to the number of conjugate base molecules when the pH = pK_a:

pH = pK_a + log ( [Base] / [Acrid] )
if [Base] = [Acid], then
pH = pK_a + log 1
pH = pK_a

Because the conjugate acid and cohabit base molecules are available in equal amounts when the pH = pK_a, the buffer solution has the strongest ability to protect confronting pH changes caused past incoming H₃O⁺ or OH^– ions when the pH of the solution is close to the pK_a of the conjugate acid. If the pH of the solution strays likewise far from the pK_a indicate, the buffer uses up all its available cohabit acrid or base molecules, and the pH starts to fall (or rise) dramatically. At this point, the buffering capacity of the buffer has been exceeded. this can be seen in the buffer (weak acid) titration graph below.

Buffers protect the pH of a solution best within one pH unit of the pK_a.

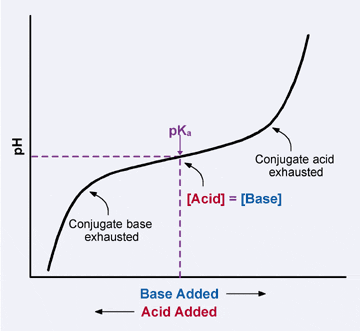Buffer titration: within one unit of the pKa, the solution resists changes in pH.

Buffers are of import for biochemistry because the structures (and therefore the functions) of biological molecules are stable inside a relatively narrow range of pH values.The evolution of life, which is believed to have begun in h2o, was likely due in office to the stable pH of seawater. Even today, the largest buffered systems in the world are the World's oceans. Carbon dioxide (CO₂) from the Globe'southward atmosphere reacts with H₂O to produce carbonic acid, H₂CO₃. Carbonic acrid in plow reacts with water to form bicarbonate:

H2CO3	+	H2O		HCO3 –	+	H3O+
carbonic acid		h2o		bicarbonate ion		hydronium ion

Furthermore, the bicarbonate ion can too react with water to grade carbonate:

HCO3 –	+	HiiO		CO3 2–	+	H3O+
bicarbonate ion		water		carbonate ion		hydronium ion

The carbonate and bicarbonate ions act together as cohabit acid/base pair to continue the pH of the body of water at about eight.ii.

In the living organisms, proteins (the molecules which exercise most of the "work" of a cell) are very sensitive to acid concentration, considering they simply fold into their proper iii-dimensional shapes within a small pH range. Some of the individual amino acid building blocks that brand upwardly a protein have ionizable side chains that change their ionization state, or charge, at different pH. Thus, if the pH changes, some of the attractive forces that hold the protein together will also change.

The ionization states of the side concatenation of the amino acid lysine are shown below. The pK_a of lysine'southward side chain amino group is approximately 10.viii. Therefore, at a pH lower than the pK_a, the side chain is in the protonated (conjugate acid) state; whereas at a pH college than the pK_a, the side chain is unprotonated (cohabit base of operations).

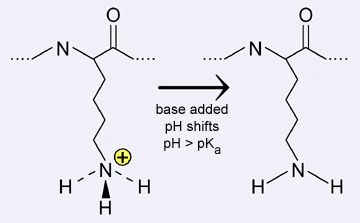Amino acrid accuse changes: if the pH of the environment around a basic amino acid shifts so that it is greater than the pKa, the amino acid is deprotonated, no longer carries a charge, and is unable to course ionic bonds.

Proteins consist of long chains of amino acids, many of which include acidic or basic groups. These groups are chaged at physiological pH, and form ionic interactions with each other that contribute to the stability of the folded protein. A change in pH of the protein'southward aqueous surroundings may alter the charge of some of these charged groups, disrupting the ionic interactions and the stability of the protein'southward structure.

Call back that the Henderson–Hasselbalch equation was used for computing the pH of a solution containing a weak acrid and its cohabit base. Since such a solution is a buffer, the Henderson–Hasselbalch equation is extremely useful for calculations involving buffers, allowing the following:

• Determination of the pH of buffered solutions.
• Decision of the ratio of conjugate base to conjugate acid at a given pH.

Instance vii

A solution of lactic acid has twice equally many cohabit acid molecules equally conjugate base molecules. If the pK_a of lactic acid is 3.85, what is the pH of such a solution?

Answer:

Nosotros are given that the concentration of cohabit acid is twice the concentration of conjugate base of operations. Thus,

[acid] = 2 [base]

Substituting into the Henderson-Hasselbalch equation:

pH = pK_a + log ([base of operations]/[acid])
pH = 3.85 + log ([base]/2[base])
pH = 3.85 + log (0.5)
pH = iii.85 + (–0.30)
pH = three.55

---

Source: https://sceweb.sce.uhcl.edu/wang/biolab/acid_base/7_buffers.html

Posted by: ballardloffinds.blogspot.com

Share this post